Welcome
Microwave background radiation indicates that the universe has a center
Author: Otakar Svoboda
Used nomenclature: universe = whole universe; cosmos = from the Earth observable part of the universe; space = outer space where the universe is expanding if there.
1. Introduction
Although there were various cosmological theories and models, scientists now commonly respect the standard model of cosmology adhering to the cosmological principle claiming that overall the universe looks the same and has no specific center.
But so far, no one noticed that the current combination of temperature and age of the universe contradicts this model. It is not difficult to prove this contradiction by tracking the universe's expansion during the era of mass with defined limit temperatures. Respective calculations (and conclusions resulting from them) follow.
2. Calculations
The universe expands and cools. Its volume has to be inversely proportional to its temperature. Microwave background radiation shows the current temperature of the universe 2.73º K. The drop of temperature from 3000º K to 2.73º K during the era of mass corresponds to 1099−fold increase in volume. This is equivalent to 6.4018−fold extension of the universe's diameter.
The 6.4018-fold extended diameter (radius) means that if there was any source emitting radiation at the time when the universe was hot 3000º K and 1099-fold smaller (at the beginning of the era of mass) which would be detected on the Earth now, then the radiation would show the red shift z = 6.4018. Due to this red shift the Earth and the source would be considered as receding one another with the speed of 6.4018*c. The highest theoretically possible acceleration of any movement during the era of mass is the speed of light and therefore the shortest possible time necessary to reach the speed of 6.4018*c (the red shift z = 6.4018 for radiation) is 2*6.4018 = 12.8036 Gyr. In other words, photons emitted 12.8036 Gyr ago and detected on the Earth now would traverse 12.8036 Gly extended for a further 12.8036*6.4018 = 81.966 Gly by the expansion of the universe to 94.7696 Gly (Ho = 76.378 km/sec per Mpc). This corresponds to the now used equation for calculation of distances of cosmic objects R = Ro*(z + 1) (but we will see that this equation can not apply generally). Note that you obtain the same result from the equation for uniformly accelerated motion R = vo*t + 0.5*a*t² = 12.8036 + 0.5*12.8036² = 12.8036 + 81.966 Gly when the vo = a = 1 Gly/Gyr (it is in both cases the speed of light in used units; nobody will surely doubt that even in the time of the transition from the radiation era to the era of mass radiation had to be emitted at the speed of light - in the era of mass also the maximum possible acceleration). And so the sum of 81.966 + 12.8036 = 94.769 Gly would have to be the current total distance of the source from the Earth. To overcome such a distance exclusively by the expansion with the maximum possible acceleration would take √94.769*2 = 13.767280 Gyr. To this time is only necessary to add another 380000 years for the period to the imputed Big Bang (during which the temperature of the universe dropped to 3000º K) to have the age of the universe proved by CMB.
It is important that the above from the MCB calculated period of the era of mass (which is approximately the age of the universe) 13.767280 Gyr corresponds to the age of the universe 13.7 ± 0.2 Gyr determined on the basis of other observations because it proves that in the real universe must apply for this case
Ro*(z+1) = vo*t+0,5*a*t².
This equality shows not only the correctness of the used premises and calculations but also that the expansion of the real universe throughout the era of mass could not be other then the uniformly accelerated at the theoretically maximum possible acceleration. (For example, if the universe's expansion would decelerate for 7 Gyr due to gravitation and then accelerate till today due to dark energy as it is now claimed, then the universe would have to be either significantly older or the speed of light in vacuum could not be constant, both of which are excluded). But it denies validity of the cosmological principle on large scales (and therefore of the current standard model of cosmology based on it) because the uniformly accelerated expansion of the universe requires one center of expansion. The calculated total distance 94.769 Gly represents (with sufficient accuracy) the current distance of the Earth from this center of the expansion, i.e. from the center of the universe (or imputed "Big Bang" or "collision" if any occured). This distance accounts for only part of the total length of the actual universe's radius. The cosmos (which we see) has a shape of a rotational body (area) around the axis proceeding from the center of the universe (which is one pole of the from the Earth visible area) in the direction of motion of the Earth (with our galaxy) due to expansion. Homogenous distribution of mass on large scales (if it is) is possible, but this type of expansion means that each cosmic object (gravitationally bound system) must move from the center of the universe along radius which is not identical with the path of photons detected on the Earth (if the source is not exceptionally located on the same radius as the Earth), and therefore distances calculated from detected magnitudes are mostly inaccurate (determining the length of path of radiation toward the Earth, not the path of the source) when directions of observations are not taken into account (as it is common). This also applies to Type 1a supernovae used as ”standard cosmic candles”. Supernovae with different red shifts observed now in one direction (or at least in one very narrow field, for example in one Hubble deep field) have different pathways. Situation of model supernovae in one randomly selected direction is schematically shown in Figure 1.

Fig. 1. Schema of positions of differently old model supernovae which would be now observed in one direction
There are also shown distances of model supernovae from relevant positions of Earth at the time of explosion (the most distant was supernova with the red shift z=1 which situation is indicated in Fig. 1 by arrows, and which therefore must appear relatively less bright) and paths of light to the actual position of the Earth. We also see that wherever we look in the cosmos our view (leading necessarily back in time) turns always at the end into a single point which is the center of expansion (center of the universe) with calculable coordinates.
The single-center universe allows to construct a graph of dependency of age (t), red shift (z) and medium distance R as shown in Figure 2. Distance is expressed by the way of a middle distance modulus (m-M) = 25+5*log(153.2802*t²).

Fig. 2. Dependance of age, red shift and middle distance modulus
Graph in Fig.2 shows the principle but is exactly applicable only for SN which were at the time of explosion as far away the center of expansion as the place of Earth. (Note that the curves are most distant at z=1.)
Similarly, you can construct model graphs for the maximum and minimum possible distance. All real SN must have their (m-M) within this range (on the nearside towards the maximum, on opposite side towards minimum). But for accurate determination of parameters of the real observed SN you need to locate the center of expansion (knowing the distance of the center from the Earth is not enough), and so to determine the origin of the coordinate system of the universe enabling reliable determination of position, distance and age of any shining cosmic object only from easily measurable red shift (taking into account the direction of observation). The Earth's coordinates in this system are: x=0, y=94.769Gly, z=0.
3. How to locate the center of the universe
The figures elucidate possible way of localization of the origin of the coordinate system of the universe (i.e. of the center of the universe) by using Type 1a supernovae. The Earth, the center of the universe and an appropriate remnant of an individual supernova form always a triangle. All triangles have the same two peaks (positions of the Earth and the center) and one side (the during the previous calculated distance of the Earth from the center 94.769 Gly). Other elements of each individual triangle can be easily calculated from the red shift, direction of observation (right ascension, declination), mean possible distance and the distance calculated from the measured magnitude of the supernova (the difference between the mean possible distance and the distance calculated from the magnitude by Pogson’s equation allows to determine the angle between the tracks of appropriate supernova and Earth). But reliable localization of the center of expansion (and the path along which the Earth is moving away from said center) needs accurate initial data (magnitudes, red shifts) of distant Type 1a supernovae observed in at least three distinctly different directions. Adam G. Riess et al. present in (1) data on supernovae discovered in two Hubble deep fields. Two directions are not enough, however, supernovae SN 1997ff and SN 2003 (the outermost supernovae in individual directions in the cited article) evoke that we could look straightforwardly to the center of the universe distant 94.769 Gly observing the region of the sky around the right ascension and declination 21h; 30º (or conversely 9h; -30º because two concentric circles of the possible directions still have two intersections), but only preliminary because it is necessary to evaluate a larger number of cosmic candles. Anyone who has access to such data has the opportunity to correct it.
4. Results
The microwave background radiation proves that the universe has a center from which it expands for 13.768 Gyr (rounded to three decimal places) with the permanently highest theoretically possible acceleration (it also reveals the only one possible future of the universe). A coordinate system of the universe and the coordinates of the Earth in it are defined. The center of the universe (the origin of the defined coordinate system) is now distant 94.769 Gly from the Earth in a direction determinable using Type 1a supernovae as ”standard cosmic candles”. But it excludes validity of the now generally recognized cosmological principle on large scales (in fact the mere expansion of the universe contradicts it); the standard model of cosmology requires an appropriate modification.
With questions, comments or for further information, please contact the author: otakar.svoboda@volny.cz 8/9/2013
References
(1) Adam G. Riess and al.2007, New Hubble Space Telescope Discoveries Of Type 1a Supernovae At z>1: Narrowing Constraints On The Early Behavior Of Dark Energy, , Astronomical Journal, 659:98-121, 2007 April 10.
Europeann Space Agency (ESA) published the map of the cosmic microwave background radiation acquired by ESA's Planck space telescope:

As for our model of expansion discussed in the opening article the found asymmetry of the hemispheres represents the next excellent proof of the existence of the center of the universe. But detected hemispheric asymmetry of the cosmic microwave background radiation does not show asymmetry of temperature as it is now claimed, but reflects the contemporary speed of move of the Milky Way (with the Earth and the probe Planck) from the center of the universe due to expansion, and so that the from all directions incoming MCB (the wavelength of which is correlated with the temperature, and so with the universe's volume) was detected by in one direction moving detectors (Doppler effect). To deduce the move of the probe Planck to the sun and of the sun to the center of the galaxy is not enough. The in today's terminology said "cooler" hemisphere is the to the center near one, the „warmer one“ is the averted.
APPENDIX 2 added on: 16/9/2013
Showcasing of expansion of the universe
Popularizing their field cosmologists usually showcase the three-dimensional expansion of the universe on the example of the two-dimensional distancing of points marked on the surface of an inflating rubber balloon because the three-dimensional expansion of the universe respecting the cosmological principle is inconceivable and inpresentable. But this presentation shows no three-domensional expansion without the center (as claimed) but only that the center of the expansion is not on the surface of the balloon (which surely no one doubts) and that it must be equidistant from all points on the surface (i.e. in the center of the balloon).
On the other hand presentation of the three-dimensional expansion of the one-center universe (described in the opening article) is easy because such an universe must expand in principle as a closed rubber balloon placed into surrounding vacuum. The apart receding points on the surface of the balloon represent only a set of points equidistant from the center and one must take into account relocation of “points” throughout the whole volume of the balloon (each point moves from the center of the balloon along its radius, the further away from the center, the faster; cosmologists unwittingly demonstrate such an expansion of one universe's diameter stretching a rubber thread with an odd number of equally spaced knobs believing that the middle knob represents the Earth when in fact it represents the immobile center of the expansion whilel the Earth represents one of the other knobs).
Imagining that a "point" located in the quarter of the radius of the balloon represents the Earth (see Fig. 1), one must only eliminate the retarding influence of an elasticity of the balloon, use other parameters (including maximum possible speed and acceleration), take into account time factor (the finite speed of light and that he observes the situation from the moving Earth) to transfer that concept to the universe.

Fig. 1 Earth location
We have to diferentiate terms cosmos and universe (and possibly Outer space, too) as shown on schematic cross section in Figure 2. There is also noticeable that the cosmos is a small part of the universe. The percentage is possible to calculate. Necessary parameters for it: the age of the universe, the way of its expansion, the distance of the Earth from the center of the universe are clarified in the opening article, and volumes of the cosmos and of the universe are so calculable.

Fig. 2 Schematic cross section of the universe
The model balloon inserted into the vacuum creates a system with a low entropy. Any system with the low entropy must pass by the laws of physic into a state of a higher entropy (unless there are fixed obstackles), i.e. must perform work (balloon must expand). If you strip away the elasticity of the balloon, the paralel with the expansion of the universe into outer space is obvious. Here is indifferent whether outer space (possibly with other universes) really exists or if it is only a metaphorical expression. Important is that MCB proves (inter alia) that the universe is expanding without any external resistence and that this means that the universe's expansion was, is, and will be uniformly accelerated. It also suggests that searching of a new type of an enigmatic additionally generated repulsing energy accelerating expansion of the universe since the middle of its age may be futile.
APPENDIX 3 added on: 26/9/2013
Fine structure constant - another evidence of the center of the universe
The dimensionless fine structure constant, a fundamental physical constant characterizing the strength of the electromagnetic interaction, was introduced by Arnold Sommerfeld in the year 1916. Its currently accepted value is 1/137.035999. As a constant it should have the same value everywhere in the universe (although some physicists pondered about it).
In the year 1999 a team of the University of New South Wales led by John. K. Webb evaluated a data set of 128 quasars and found deviations in the value of this constant on large scales. Finally, in an article published in 2011 (1) authors announced finding not only temporal but also directional dependance of deviations of fine structure constant (see Fig. 1.).
(Image copyright Dr. Julian Berengut, UNSW, 2010. May be used with appropriate attribution)

Fig. 1. Directional shift of spectral lines of radiation from quasars (credit John K. Webb et. al.)
Found deviations of the fine structure constant challenge both the physic and stability of mass. It would be a big problem needing explanation. The universe with the center of expansion, as derived in the opening article of this website, ofer it.
In the universe with the center of expansion (now distant 94.767 Gly from the Earth), where the cosmological principle is invalid on large scales, is everything simple. The physic is not compromised because needed Doppler's effect is nothing new. In one-center universe the Earth (together with the whole Milky Way) has to move due to expansion from the center and evaluating radiation from the quasars requieres to take into account the Doppler's effect together with the directions of observations. Deviations of fine structure constant then do not exist and, on the other hand, the fine structure constant could be other useful base for location of the center of the universe (like the luminosity of supernovae type 1a or the Planck's map).
The "found spatial deviations" of the fine structure constant therefore show (similarly as the alleged "hemispheric asymmetry of temperature of the universe" discussed in appendix 1) that the current standard model of cosmology accepting the cosmological principle is incorrect and that the respect for it, it is disregard for the existence of the center of the universe, brings for cosmologists a number of problems, for example how to explain: why luminosity of old supernovae type 1a (used as "standard cosmic candles") disagree with expectation, why their luminosity is relatively small in a red shift about 1 and why supernovae type 1a have such a variability in Magnitude M when they must explode reaching the Chandrasekhar's limit, why Hubble constant resulting from each further observation is a little different or, newly, problems to interpret the "hemispheric asymmetry of the universe's temperature" (not existing in fact) or "dark flow" (see Fig. 1 of the opening article showing a schematic look into past), and so on. As for the "dark matter" see the following new appendix 4.
References
J. K. Weeb1, J.A. King1, M.T. Murphy2, V.V. Flambaum1, R. F. Carswell3 and M. B. Bainbridge1, Indications of a spatial variation of the fine structure constant, Phys. Rev. Lett., 107, 191101,2011, 1- School of Physic, University of New South Wales, Sydney, NSW 2052, Australia; 2- Centre for Astrophysic and Supercomputing. Swinburne University of Technology, Mail H30, PO Box 218, Victoria 3122, Australia; 3- Institute of Astronomy, Madingley Road, Cambridge, CB3 0HA, England.
added on: 17/7/2016
Correct Value of the Hubble Constant
Introduction
Universe is expanding. The rate of it is characterized by the Hubble constant (Ho) value of which is still not exactly fixed. Values published during recent years range from 50 to 80 km*secˉ¹/Mpc as on a chart published on the www.cfa.harvard.edu) (2):
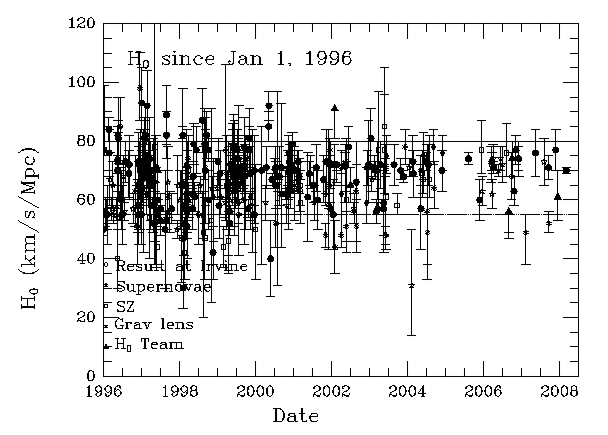
Attempts to clarify the value of Ho continue, the last one was published in April of this year (1).
Published values of Ho are usually based on observations of very distant celestial objects. Difficulties associated with these observations together with the differences between „cosmic candles“ are often considered the possible cause of the found differences (but no one still satisfactorily explained why should be such a big differences between the „cosmic candles“ of the same type, for example of the type 1a supernovae, which all have to explode reaching the Chandrasekhar's limit).
But there is a possibility to avoid these uncertainties by the way of a direct calculation of the Hubble constant from the temperature of the universe (in conjunction with the speed of light).
Calculation of the Hubble constant from the temperature of the universe
Already in the opening article was shown that light emitted 12.8036 Gyr ago, if detected on the Earth now, overcame distance 94.7696 Gly (namely 12.8036 Gly due the speed of light and 81.966 Gly due to expansion of the universe), and would have the red shift z = 6.4018. These are all of the data needed to calculate the Hubble constant, i.e. the distance 81.966 Gly (25127.529 Mpc) and the speed 6.4018*c. Dividing them we obtain:
Ho=1919211.357km*secˉ¹/25127.53 Mpc=76.378km*secˉ¹/Mpc.
Discussion of the chart on www.cfa.harvard.edu
We see that calculated Ho = 76.378 km*secˉ¹/Mpc corresponds to the upper limit value of Ho on the chart, while the lowest are about 30 km*secˉ¹/Mpc smaller. Such a big range of values (as well as their distribution) indicates that differences are probably not a consequence of any inaccuracies associated with the observation, but rather an evidence of the fact that some variable was not taken into account. Anyone who read the opening article already suspects which one. Nevertheless, a brief recap follows.
In the article was shown that radiation emitted 12.8036 Gyr ago and detected on the Earth now had to: overcame 94.7696 Gly (in that 81.966 Gly by the expansion); that it would exhibit z = 6.4018; that it was only possible if the expansion of the universe is uniformly accelerated at the during the era of mass maximum theoretically possible acceleration; that the point of its emission had to be clearly defined (and very close to the starting point of the expansion of the universe, i.e. practically of the center of the universe); that each an individual object travels from the center due to expansion along a different radius; that consequently the tracks of the Earth, the source as well as of the emitted radiation (from the source to the Earth) differ and simple summing of the expansion and the track of light may be used only for objects between the Earth and the center, and in all other cases must be used a vectorial sum (which must be alwayes smaller).
It follows that the smaller the vector sum, the lower the value of Ho (with the lowest value possible 55.741 km*secˉ¹/Mpc).
It shows that the reason of the large variance in previous values of Ho is non-use of vectors (therefore these should be better referred as „apparent“). Non-use of vector calculus means that resulting values of Ho correspond all to distances according to the equation R=Ro(z+1) while in fact the right distances range from Ro(z+1) to Ro(z-1) (which proves that for right determination of the distance of the "cosmic candle" the direction of observation must be taken into account.
When the directions of observations of "cosmic candles" are disregarded then values of the Ho can be between the possible maximum 76.378 km*secˉ¹/Mpc an the minimum 55.741 km*secˉ¹/Mpc and results show (according to the laws of statistic) the Gausian distribution which can lead to an erroneous assumption that the correct universally valid Ho should be a peak of the Gaussian curve whilem, in fact, it is only the mean value, and the right value characterizing the expansion of the universe in the radial direction in a given time is the upper limit 76.378 km*secˉ¹/Mpc.
Finally, differences in previous values of the Hubble constant and their distribution corresponding exactly to the laws of statistic are actually further proof of the existence of the center of the universe.
References
-
Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; Casertano, Stefano; Filippenko, Alexei V.; Tucker, Brad E.; Reid, Mark J.; Jones, David O. (2016-04-05). "A 2.4% Determination of the Local Value of the Hubble Constant".
-
www.cfa.harvard.edu; „The Hubble Constant“
www.universum2.webnode.cz
This list is empty.
Tags
The list of tags is empty.
News
———
———
